Lab 4&5: Mazes - Depth and Breadth First Search

Overview

In this lab, we will implement generic versions of the Stack and Queue data types within the context of searching a maze.

Materials

• IntelliJ
• Lab partner

Setup

1. Download the skeleton for this project.
2. Extract the code, then open the maze151dfsbfs folder in IntelliJ to start a new project.

Description

In this lab, we will explore searching a maze for a goal using stacks and queues to organize our potential Trails. The stack allows us to search in a depth-first search manner. In other words, we can explore down a trail as far as possible, and backtrack if we reached a dead end in our journey, because we search the youngest potential trail next. While the queue will allow us to search in a breadth-first search manner, always exploring the oldest potential trail next.

In this lab, you will create the necessary data structures to search a maze in these two ways

To start, run the code in MazeApp. You should see the GUI layout here.

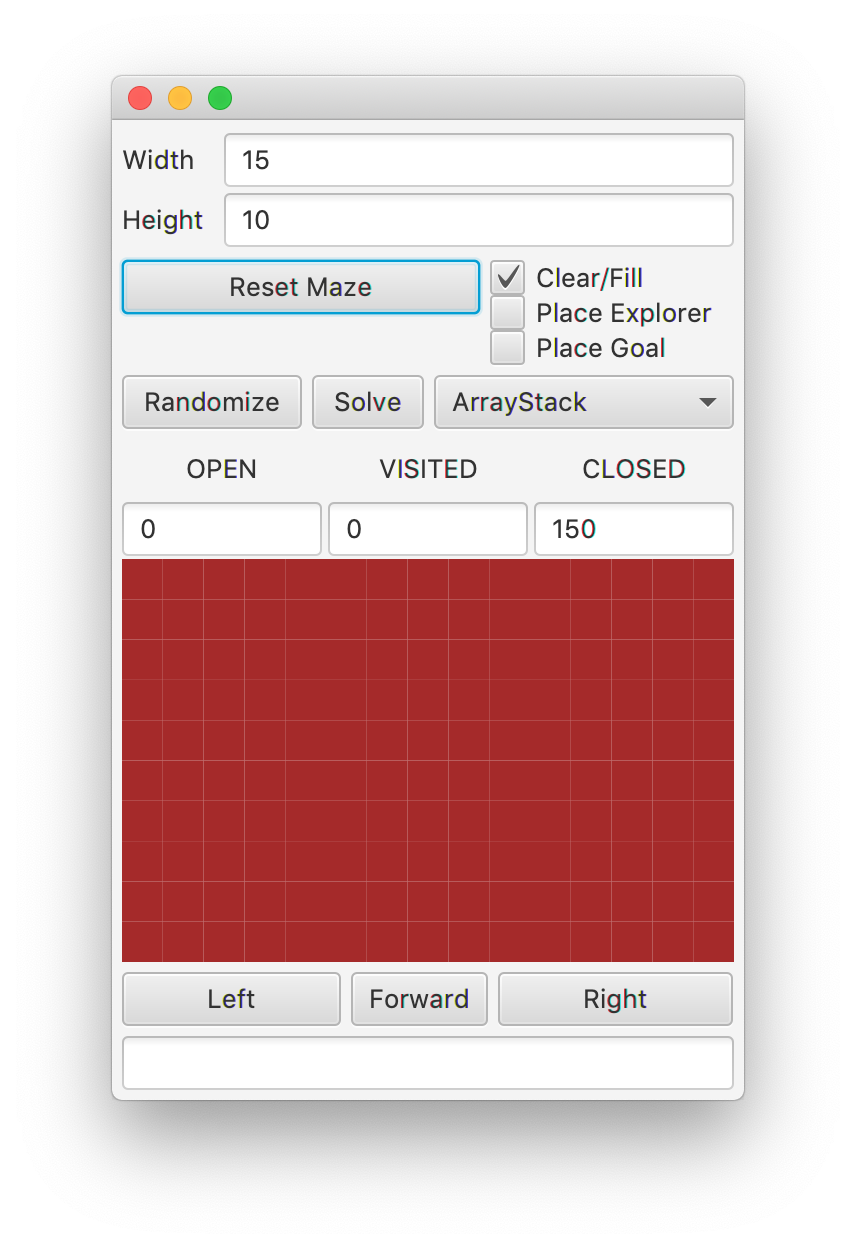
There are a few new pieces to this GUI. First, you will see a choice for either ArrayStack, ListStack, ArrayQueue, or ListQueue. You will find the starter code for these included in the maze.searchers directory.

Second, you will notice that there are statistics in the middle portion of the GUI, recording the number of OPEN, CLOSED, and VISITED squares.

Third, there is a box at the bottom, to report errors when things go wrong with the underlying implementations. It will also report the number of steps taken when a solution trail is found through searching.

Stacks

Our first task is to implement a generic Stack interface that can be used in many pieces of the code, for generating and then solving mazes.

Step 1 - ArrayStack<E>

Write a class called ArrayStack<E>. This will need to implement the Stack<E> interface. The fields and constructor are provided for you.

Step 1.1 - public void push(E item)

If there is no more room in the stuff array, you will need to resize.

• Create a new array twice as big as stuff.
• Copy over each item into the new array.
• Redirect the stuff reference to the new array.

Now, you can always add the new item to top spot in the stuff array, and increment the top.

Step 1.2 - public E pop()

Call the emptyCheck method. This will throw an IllegalStateException if the stack is empty.

Decrement the value of top, and then return the item in the top spot of the stuff array.

Step 1.3 - public E peek()

Call the emptyCheck method. This will throw an IllegalStateException if the stack is empty.

Return the item in the top - 1 spot of the stuff array.

Step 1.4 - public int size()

Return the number of items in stuff.

Step 1.5 - public String toString()

Return a String representing the elements in the stack separated by spaces. For example, a stack of integers with 3 on top of 2 on top of 1 should return “1 2 3”. The oldest element in the stack should be the first in the string.

Step 1.6 - Testing

Run the ArrayStackTest suite, and ensure your above methods are passing these tests.

Step 2 - ListStack<E>

Next we will implement the generic version of a Stack with nodes, called ListStack<E>. This will need to implement the Stack<E> interface, and have at least a ListNode<E> called top as a field.,

Step 2.1 - ListNode

Look over the file called ListNode.java. This class implements the Node class we discussed. It should have an E value and a ListNode next reference as private components, along with public get and set methods for the value and next fields. There are two constructors. The first brings in and stores only an E value, and leaves the ListNode next as null. The second brings in both an E value, and a ListNode next, storing both.

Step 2.2 - public void push(E data)

Study the code provided. It will create a new ListNode that stores the data, has the current topas its next, and finally redirects top to reference this new ListNode.

Step 2.3 - public E pop()

Call the emptyCheck method. This will throw an IllegalStateException if the stack is empty.

Save the value stored in top, and redirect top to point to the next ListNode.

Return the value you stored.

Step 2.4 - public E peek()

Call the emptyCheck method. This will throw an IllegalStateException if the stack is empty.

Return the value stored in the top ListNode.

Step 2.5 - public int size()

If top is null, return 0. Otherwise, return the number of ListNode that are chained from the top node.

Step 2.6 - public String toString()

Return a String representing the elements in the stack separated by spaces. For example, a stack of integers with 3 on top of 2 on top of 1 should return “1 2 3”. The oldest element in the stack should be the first in the string.

Step 2.7 - Testing

Run the ListStackTest suite, and ensure your above methods are passing these tests.

Queues

Step 3 - ListQueue<E>

To implement the generic version of a Queue with nodes, you should use the generic ListNode<E> class we implemented last lab.

Step 3.1 - Implementation

Write a class called ListQueue<E>. This will need to implement the Queue<E> interface, and have at least a ListNode<E> called front and another called back as fields.

Step 3.2 - public void add(E item)

Create a new ListNode<E> that stores the item.

If the queue isEmpty, then set front to this new ListNode<E>.

Otherwise, the current back should refer to this new ListNode<E> as its next.

Finally, redirect back to reference this new ListNode<E>.

Step 3.3 - public E remove()

Call the emptyCheck method. This will throw an IllegalStateException if the queue is empty.

Save the value stored in front, and redirect front to point to the next ListNode<E>.

Return the value you stored.

Step 3.4 - public E element()

Call the emptyCheck method. This will throw an IllegalStateException if the queue is empty.

Return the value stored in the front ListNode<E>.

Step 3.5 - public int size()

If front is null, return 0.

Otherwise, return the number of ListNode<E> that are chained from the front node.

Step 3.6 - Testing

Run the ListQueueTest suite, and ensure your above methods are passing these tests.

Step 4 - Creating Random Mazes

You should now be able see new mazes when you click the Randomize button.

Run the GUI to interact with your code and make random mazes. You should see mazes similar to the image below.

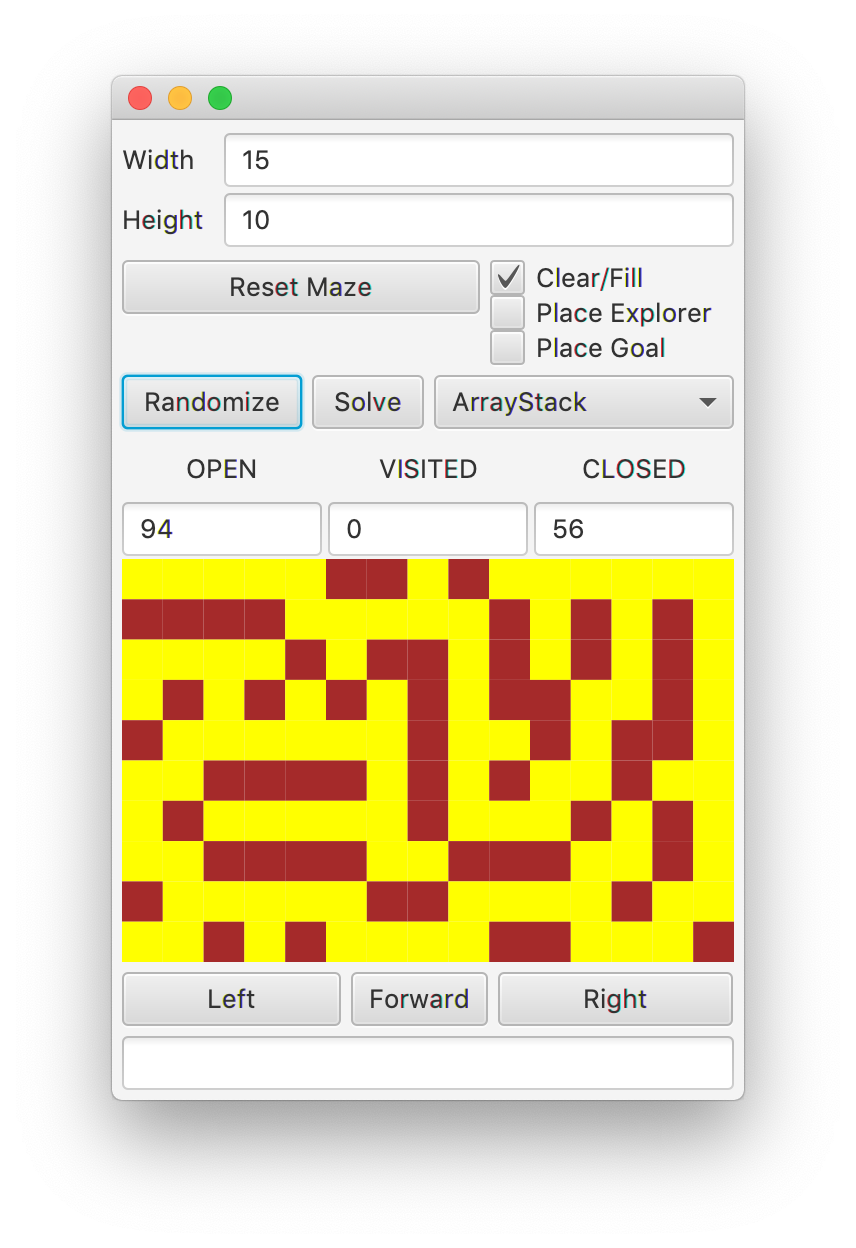
Step 5 - Solving Mazes

A Trail is another recursive data structure, similar to a ListNode. The two fields of a Trail are a Position, denoting the end of the trail, and a link to another Trail called prev, which is a record of how you arrived at the current Trail. For the first step of a Trail, the prev is left as null.

In this step, you will use Trails to write an algorithm in the Puzzle class that solves a maze using either a Stack or a Queue. This is because the behavior of both is abstracted into a Searcher class. The Searcher class has method names like the Queue.

Step 5.1 - public Trail solve(Searcher<Trail> solver)

If there is no Explorer in the maze or no goal in the maze, then return null.

Otherwise, add a new Trail starting at the Explorer’s position onto the solver.

While the solver still has potential Trails:

• Remove the next Trail from the solver.
• If the Trail end is the goal Position, return this Trail
• If the Cell in the Maze at the Trail end is OPEN
  • Mark it as a VISITED Cell
  • Add new Trails based on this Trail for each of the neighbors to the solver.

If you empty the solver and have still not found the goal, then return null.

Step 5.2 - Testing

Run the PuzzleTest suite, and ensure your above methods are passing these tests.

Step 5.3 - GUI

Run the GUI to interact with your code. When you Randomize to create a random maze, add an Explorer and goal, and then click the Solve button, you should see something similar to the following image.

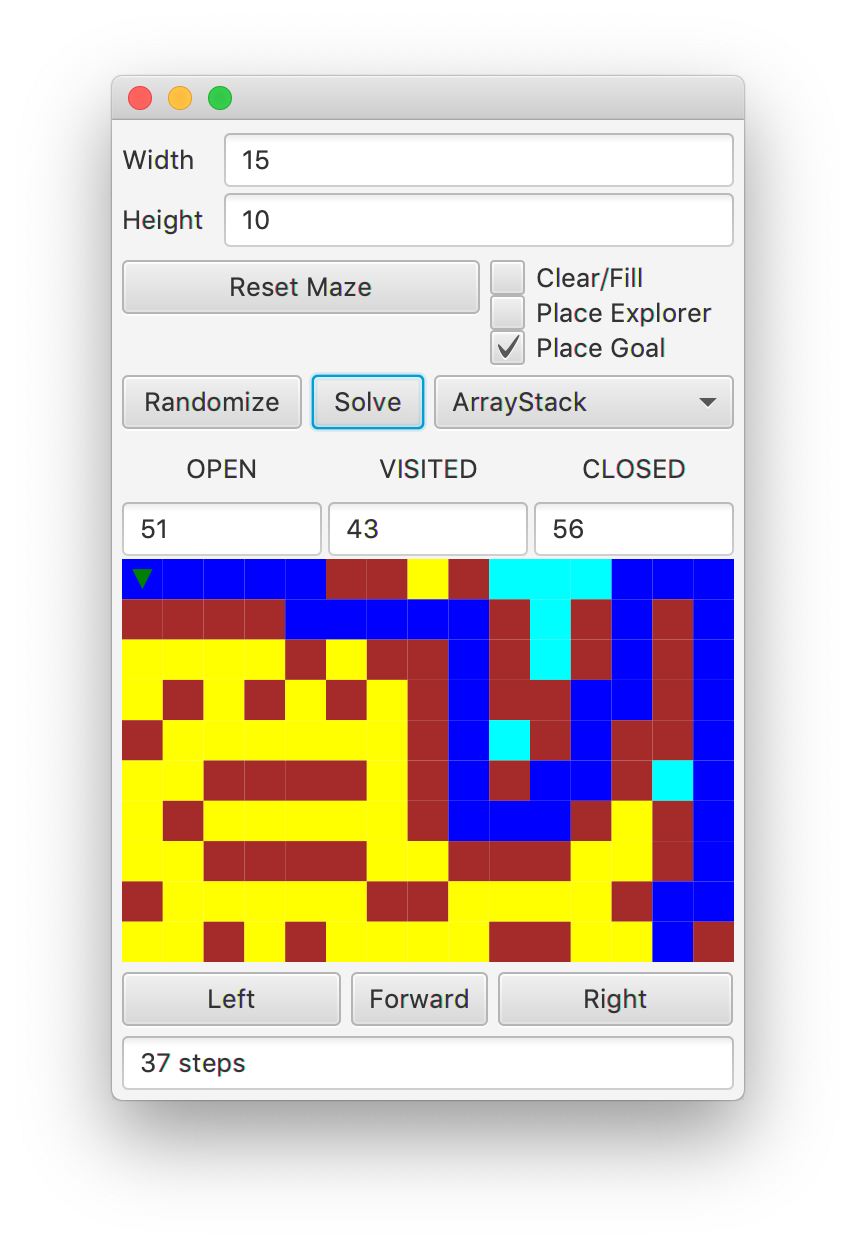
Step 6 - Evaluation

Create 10 mazes of size 30x30 and record the number of visited nodes as a percentage of the total number of open spaces in the initial maze. Also, record the number of steps used by your solver. You can choose either implementation for each data type.

Use this data to compare the Stack versus Queue search strategies. Does either strategy have any clear strengths or weaknesses?

Grading

• To Complete this lab, complete all the steps.